Standard Deviation

Standard Deviation

Calculation of Standard deviation

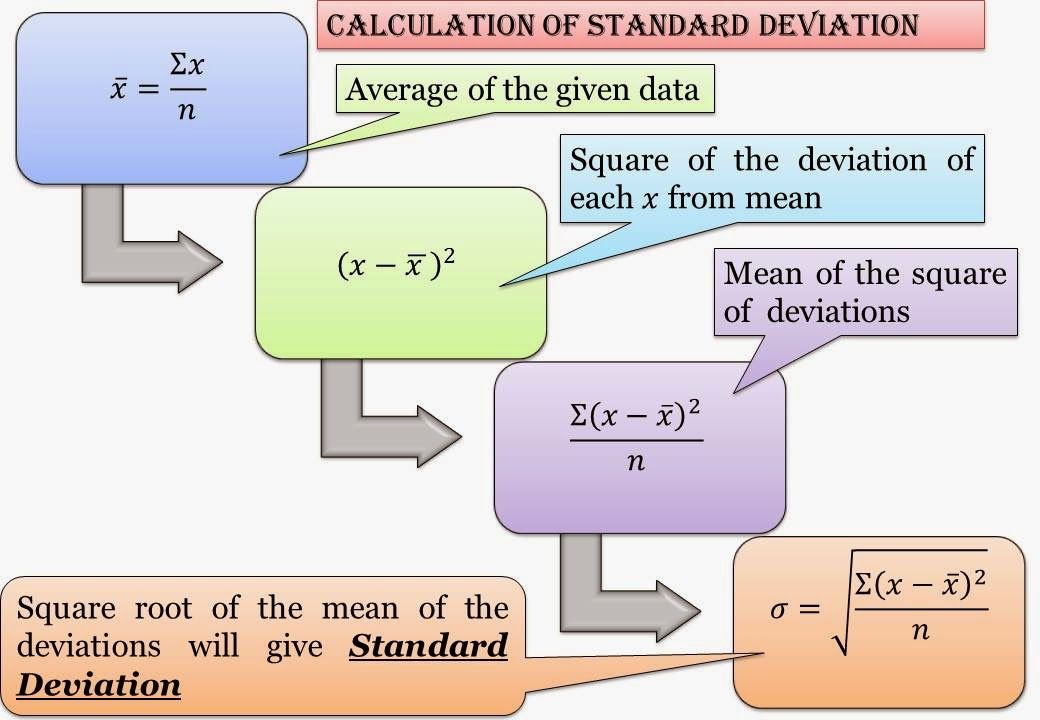
Standard deviation is defined as the square root of the arithmetic mean of the squares of the deviation of the values taken from the mean. It is denoted by small Greek letter read as ''sigma''. 

Calculation of standard deviation can understand by the fig. and mentioned below 

let 

X = X1, X2, X3, X4, ............................Xn

Xbar = (Sum of All Xn)/n

Now calculate the square of the deviation from each X from Xbar and then  calculate the mean of square of the deviations given as 

Sum(Xn-Xbar)^2/n

Now find the square root of this value and find the standard deviation of the data

Hence Standard deviation= square root(Sum(Xn-Xbar)^2)/n

Population Standard deviation

When sum of square deviation is divided by n then it is the population standard deviation

Sample Standard deviation

When sum of square deviation is divided by (n-1) then it is the sample standard deviation.

Difference between Mean deviation and standard deviation

1. Algebraic signs of deviations (+/-) ignored while calculation mean deviation whereas in the calculation of standard deviation signs of deviations are not ignored i.e. they are taken into account .
2. Mean deviation can be computed either from mean , median or mode. The standard deviation, on the other hand , always computed from the mean because the sum of the squares of the deviations taken from the mean is minimum.

To get Telephonic tutorials and e-book of Quantitative Techniques measure of dispersion click here